Table of contents:
Code documentation
Find here, the Yadics library documentation.
The possibilities of Yadics are summarized in the diagram below :
Yadics theoretical background
Image Registration Principle
YaDICs can be explained using the classical Image Registration framework [1] :
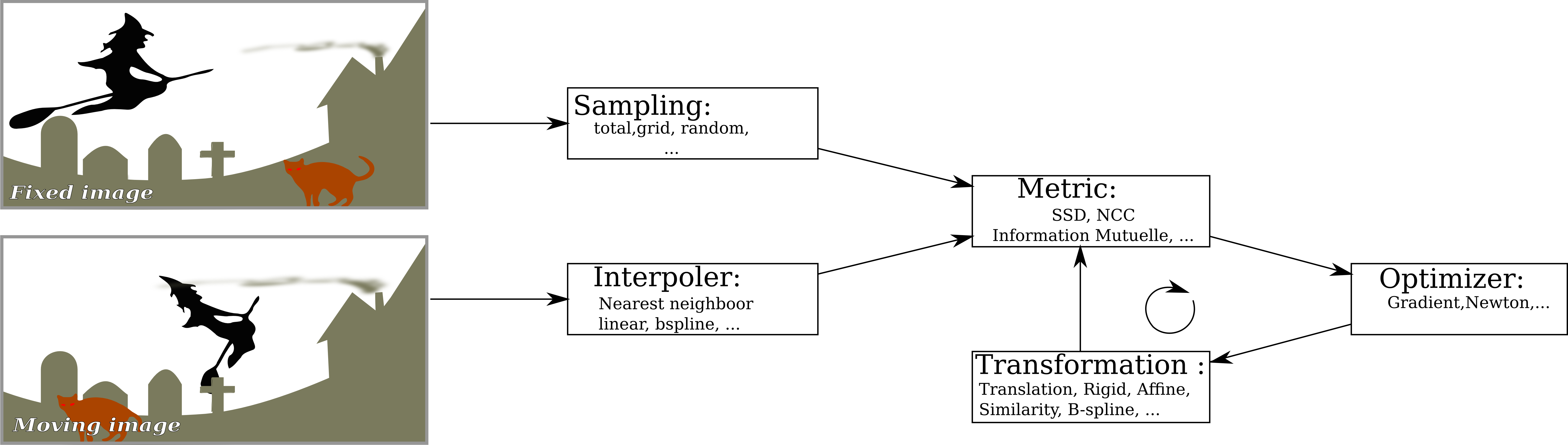
Image registration general scheme
The common idea of Image Registration and Digital Image Correlation is to find the transformation between a fixed image and a moving one for a given metric using an optimization scheme. While there are a lot of methods to achieve such a goal, Yadics focuses on registering images with the same modality. The idea behind the creation of this software is to be able to process data that comes from a µ-tomograph i.e: data cube over 1000³ voxels. With such a size it is not possible to use naive approach usually used in a 2D- context. In order to get sufficient performances OpenMP parallelism is used and data are not globally stored in memory. As an extensive description of the different algorithms is given in [1] , this documentation will only deal with the Yadics approach.
Sampling
Contrary to Image Registration, Digital Image Correlation targets the transformation, one wants to extracted the most accurate transformation from the two images and not just match the images. Yadics uses the whole image as a sampling grid: it is thus a total sampling.
Interpolator
It is possible to choose between linear and bi-cubic interpolations for the grey level evaluation at non integer coordinates. The bi-cubic interpolation is the recommended one.
Metrics
Sum of Squared differences (SSD)
The equation below defines the SSD metric :
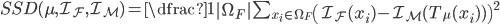
where 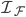 is the fixed image,
is the fixed image, 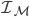 the moving one,
the moving one, 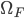 the integration area
the integration area 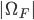 the number of pi(vo)xels (cardinal) and
the number of pi(vo)xels (cardinal) and 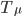 the transformation parametrized by
the transformation parametrized by 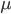
The transformation can be written as :
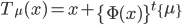
This metric is the main used in the Yadics as it works well with same modality images. One has to find the minimum of this metric
Normalized Cross Correlation (NCC)
The NCC is used when one cannot assure the optical flow conservation, it happens in case of change of lighting or if particles disappear from the scene can occur in Particule Images Velocimetry (PIV).
The NCC is defined by :

where 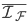 and
and 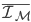 are the mean values of the fixed and mobile images.
are the mean values of the fixed and mobile images.
This metric is only used to find local translation in Yadics. This metric with translation transform can be solved using cross-correlation methods, which are non iterative and can be accelerated using Fast Fourier Transform .
Classification of transformations
There are three categories of parametrization, elastic, global and local transformation. The elastic transformations respect the partition of unity, there are no holes created or surfaces counted several times. This is commonly used in Image Registration by the use of B-Splines [1, 2] and in solid mechanics with finite element basis [3, 4]. The global transformations are defined on the whole picture using rigid body or affine transformation (which is equivalent to homogeneous strain transformation). More complex transformations can be defined such as mechanically based one. These transformations have been used for stress intensity factor identification by [5, 6] and for rod strain by [7]. The local transformation can be considered as the same global transformation defined on several Zone Of Interest (ZOI) of the fixed image.
Global
Several global transforms have been implemented :
- Rigid and homogeneous (Tx,Ty,Rz in 2D ; Tx,Ty,Tz,Rx,Ry,Rz,Exx,Eyy,Ezz,Eyz,Exz,Exy in 3D),
- Brazilian [8] (Only in 2D),
- Dynamic Flexion,
Elastic
First order quadrangular Finite Elements Q4P1 are used in Yadics
Local
Every Global transform can be used on a local mesh.
Optimization
The yadics optimization process follows a gradient descent scheme
The first step is to compute the gradient of the metric regarding the transform parameters

Gradient method
Once the metric gradient has been computed, one has to find an optimization strategy
The gradient method principle is explained below :
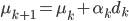
The gradient step 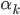 can be constant or updated at every iteration.
can be constant or updated at every iteration.
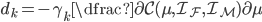 ,
, 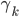 allows one to choose between the following methods
allows one to choose between the following methods
-
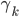 =1
=1  steepest descent,
steepest descent, ![\gamma_k=\left [ \dfrac{\partial \mathcal{C}(\mu,\mathcal{I_F},\mathcal{I_M})}{\partial \mu}\dfrac{\partial \mathcal{C}(\mu,\mathcal{I_F},\mathcal{I_M})}{\partial \mu}^{t} \right ]^{-1}](wp-content/plugins/latex/cache/tex_1b23a6c2e8f957d4baf1a027fbe16b2d.gif)
 Gauss-Newton,
Gauss-Newton,
A lot of different methods exist (BFGS, conjugate gradient, stochastic gradient, ...) but as steepest gradient and Gauss-Newton are the only ones implemented in Yadics these methods are not discussed here.
The Gauss-Newton method is a very efficient method that needs to solve a ![[M]\{U\}=\{ F \}](wp-content/plugins/latex/cache/tex_066bf5a7040e3530e306ec9195cd14c7.gif) . On 1000³ voxels µ-tomographic image the number of Degrees of Freedom can reach 1e6 (i.e: on a 12x12x12 mesh ), dealing with such a problem is more a matter of numerical scientists and required specific development (using libraries like Petsc or MUMPS) so we don't use Gauss-Newton methods to solve such problems. We have developed a specific steepest gradient algorithm with a specific tuning of the
. On 1000³ voxels µ-tomographic image the number of Degrees of Freedom can reach 1e6 (i.e: on a 12x12x12 mesh ), dealing with such a problem is more a matter of numerical scientists and required specific development (using libraries like Petsc or MUMPS) so we don't use Gauss-Newton methods to solve such problems. We have developed a specific steepest gradient algorithm with a specific tuning of the 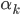 scalar parameter at each iteration. The Gauss-Newton method can be used in small problems in 2D.
scalar parameter at each iteration. The Gauss-Newton method can be used in small problems in 2D.
Pyramidal Filter
None of these optimization methods can succeed directly if applied at the last scale as the gradient methods are sensitive to the initial guests. In order to find a global optimum one has to evaluate the transformation on a filtered image. The figure below illustrates how to use the pyramidal filter to find the transformation [9].
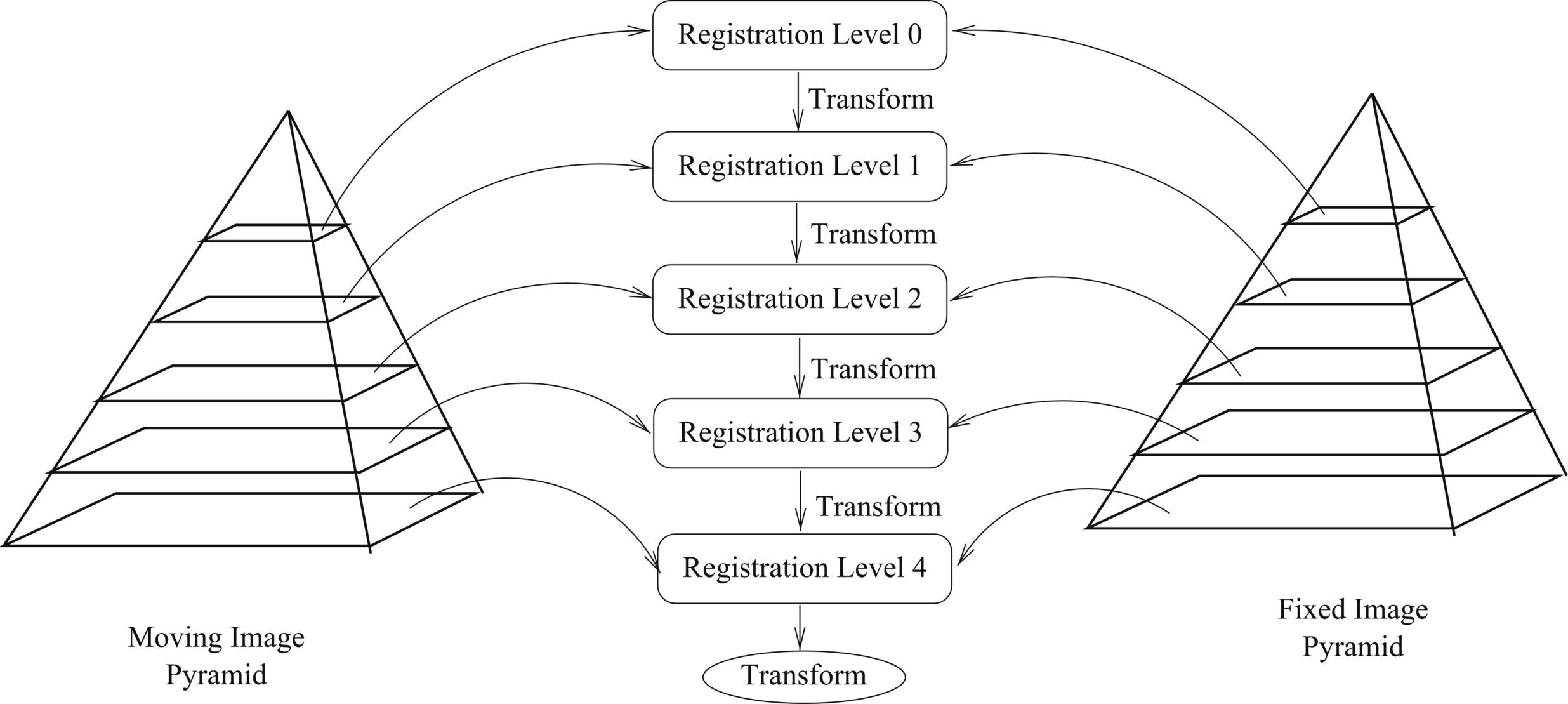
Pyramidal process used in Yadics (and ITK)
Regularization
The metrics is often called Image energy, people usually add energy that comes from mechanics assumptions as the laplacian of displacement (a special case of tikhonov regularization [10]) or even Finite Element problems. As we decided not to solve the Gauss-Newton problem for most of cases this solution is far from being CPU efficient. Cachier et al. [11] demonstrated that the problem of minimizing image and mechanical energy can be reformulated in solving the energy image then applying a Gaussian filter at each iteration. We use this strategy in Yadics and we add the median filter as it is massively used in PIV. One notes that the median filter avoids local minima while preserving discontinuities.
The filtering process is illustrated in the figure below
[Bibtex]
@ARTICLE{KleStar10,
author = {Klein, S. and Staring, M. and Murphy, K. and Viergever, M.A. and
Pluim, J. P W},
title = {elastix: A Toolbox for Intensity-Based Medical Image Registration},
journal = {Medical Imaging, IEEE Transactions on},
year = {2010},
volume = {29},
pages = {196-205},
number = {1},
doi = {10.1109/TMI.2009.2035616},
issn = {0278-0062},
keywords = {biomedical MRI;computerised tomography;image registration;medical
computing;medical image processing;public domain software;automated
data processing;command-line interface;computed tomography;elastix;intensity-based
medical image registration;magnetic resonance imaging;scripting;Application
software;Biomedical imaging;Cost function;Image processing;Image
registration;Image segmentation;MONOS devices;Open source software;Optimization
methods;Spatial resolution;elastix;image registration;medical imaging;open
source;software;Diagnostic Imaging;Humans;Image Processing, Computer-Assisted;Models,
Biological;Normal Distribution;Software},
url = {http://dx.doi.org/10.1109/TMI.2009.2035616}
}[Bibtex]
@ARTICLE{ReEl2010,
author = {R\'{e}thor\'{e}, J. and Elguedj, T. and Simon, P. and Coret, M.},
title = {On the Use of NURBS Functions for Displacement Derivatives Measurement
by Digital Image Correlation},
journal = {Experimental Mechanics},
year = {2010},
volume = {50},
pages = {1099-1116},
number = {7},
doi = {10.1007/s11340-009-9304-z},
issn = {0014-4851},
keywords = {Digital image correlation; Beam; B-splines},
language = {English},
publisher = {Springer US},
url = {http://dx.doi.org/10.1007/s11340-009-9304-z}
}[Bibtex]
@ARTICLE{BeHiRo06,
author = {Gilles Besnard and Fran\c{c}ois Hild and St{\'e}phane Roux},
title = {Finite-Element Displacement Fields Analysis from Digital Images:
Application to Portevin-Le Ch{\^a}telier Bands},
journal = {Experimental Mechanics},
year = {2006},
volume = {46},
pages = {789--803},
number = {6},
doi = {DOI:.1007/s11340-006-9824-8},
issn = { 0014-4851},
url = {http://dx.doi.org/10.1016/0262-8856(83)90064-1}
}[Bibtex]
@ARTICLE{ReRo2007,
author = {Julien R\'{e}thor\'{e} and St\'{e}phane Roux and Fran�ois Hild},
title = {From pictures to extended finite elements: extended digital image
correlation (X-DIC) },
journal = {Comptes Rendus M\'{e}canique },
year = {2007},
volume = {335},
pages = {131 - 137},
number = {3},
doi = {10.1016/j.crme.2007.02.003},
issn = {1631-0721},
keywords = {Rupture},
url = {http://dx.doi.org/10.1016/j.crme.2007.02.003}
}[Bibtex]
@ARTICLE{haRoHi2007,
author = {Hamam, Rami and Hild, Fran{\c{c}}ois and Roux, St{\'e}phane},
title = {Stress intensity factor gauging by digital image correlation: Application
in cyclic fatigue},
journal = {Strain},
year = {2007},
volume = {43},
pages = {181--192},
number = {3},
doi = {0.1111/j.1475-1305.2007.00345.x},
publisher = {Wiley Online Library},
url = {http://dx.doi.org/0.1111/j.1475-1305.2007.00345.x}
}[Bibtex]
@ARTICLE{HiRoIDIC,
author = {Fran�ois Hild and St\'{e}phane Roux},
title = {Measuring stress intensity factors with a camera: Integrated digital
image correlation (I-DIC) },
journal = {Comptes Rendus M\'{e}canique },
year = {2006},
volume = {334},
pages = {8 - 12},
number = {1},
doi = {http://dx.doi.org/10.1016/j.crme.2005.11.002},
issn = {1631-0721},
keywords = {Rupture},
url = {http://www.sciencedirect.com/science/article/pii/S163107210500210X}
}[Bibtex]
@ARTICLE{HiRoLo,
author = {Fran�ois Hild and St\'{e}phane Roux and N\'{e}stor Guerrero and Maria
Eugenia Marante and Julio Fl\'{o}rez-Ll\'{o}pez},
title = {Calibration of constitutive models of steel beams subject to local
buckling by using digital image correlation },
journal = {European Journal of Mechanics - A/Solids },
year = {2011},
volume = {30},
pages = {1 - 10},
number = {1},
doi = {http://dx.doi.org/10.1016/j.euromechsol.2010.09.007},
issn = {0997-7538},
keywords = {Digital image correlation},
url = {http://www.sciencedirect.com/science/article/pii/S0997753810001142}
}[Bibtex]
@ARTICLE{HiRoBraz,
author = {Hild, F. and Roux, S.},
title = {Digital Image Correlation: from Displacement Measurement to Identification
of Elastic Properties ? a Review},
journal = {Strain},
year = {2006},
volume = {42},
pages = {69--80},
number = {2},
doi = {10.1111/j.1475-1305.2006.00258.x},
issn = {1475-1305},
keywords = {Brazilian disk test, correlation algorithm, integrated approach, kinematic
measurements, photomechanics},
publisher = {Blackwell Publishing Ltd},
url = {http://dx.doi.org/10.1111/j.1475-1305.2006.00258.x}
}[Bibtex]
@ARTICLE{ITK2002,
author = {Terry S. Yoo and Michael J. Ackerman and William E. Lorensen and
Will Schroeder and Vikram Chalana and Stephen Aylward and Dimitris
Metaxas and Ross Whitaker},
title = {Engineering and Algorithm Design for an Image Processing API: A Technical
Report on ITK - the Insight Toolkit},
year = {2002},
pages = {586--592},
month = {01},
abstract = {We present the detailed planning and execution of the Insight Toolkit
(ITK), an application programmers interface (API) for the segmentation
and registration of medical image data. This public resource has
been developed through the NLM Visible Human Project, and is in beta
test as an open-source software offering under cost-free licensing.
The toolkit concentrates on 3D medical data segmentation and registration
algorithms, multimodal and multiresolution capabilities, and portable
platform independent support for Windows, Linux/Unix systems. This
toolkit was built using current practices in software engineering.
Specifically, we embraced the concept of generic programming during
the development of these tools, working extensively with C++ templates
and the freedom and flexibility they allow. Additional software development
tools for distributed consortium-based code development have been
created and are available from the project. In this paper, we discuss
our assumptions, design decisions, and some of the lessons we have
learned.},
institution = {National Library of Medicine, National Institutes of Health, Bethesda},
publisher = {Proc. of Medicine Meets Virtual Reality, J. Westwood, ed., IOS Press
Amsterdam},
url = {http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.2.1280}
}[Bibtex]
@ARTICLE{Tikhonov1965,
author = {A.N. Tikhonov and V.B. Glasko},
title = {Use of the regularization method in non-linear problems },
journal = {\{USSR\} Computational Mathematics and Mathematical Physics },
year = {1965},
volume = {5},
pages = {93 - 107},
number = {3},
doi = {http://dx.doi.org/10.1016/0041-5553(65)90150-3},
issn = {0041-5553},
url = {http://www.sciencedirect.com/science/article/pii/0041555365901503}
}[Bibtex]
@ARTICLE{Cachier2003,
author = {Pascal Cachier and Eric Bardinet and Didier Dormont and Xavier Pennec
and Nicholas Ayache},
title = {Iconic feature based nonrigid registration: the \{PASHA\} algorithm
},
journal = {Computer Vision and Image Understanding },
year = {2003},
volume = {89},
pages = {272 - 298},
number = {2?3},
note = {<ce:title>Nonrigid Image Registration</ce:title> },
doi = {10.1016/S1077-3142(03)00002-X},
issn = {1077-3142},
keywords = {Nonrigid registration},
url = {http://dx.doi.org/10.1016/S1077-3142(03)00002-X}
}